
We weten bijvoorbeeld nog niet precies hoe het virus zich verspreidt. Het effect van maskers wordt nog steeds betwist. Hoe nauwgezet blijven mensen de beperkende maatregelen opvolgen? Al die onzekerheden zorgen voor ruis op de voorspellingen van de wiskundige en epidemiologische modellen.
Schattingen over het aantal besmettingen en het aantal gerelateerde sterfgevallen werden de laatste maanden al te vaak bijgestuurd. Een essentiële voorwaarde om de gepaste beslissingen te kunnen nemen in deze onzekere tijden bestaat erin om goed te weten wat we niet kunnen weten.
Het reproductiegetal en de IC-capaciteit
Het reproductiegetal is één van de belangrijkste factoren om politieke beslissingen zoals het invoeren en het daarna geleidelijke afbouwen van lockdownmaatregelen te nemen. Dat getal geeft aan hoeveel personen besmet worden door iemand die het virus al heeft opgelopen. Een gedeelte van de nieuwe besmette personen ontwikkelt, gemiddeld na twee weken, zware symptomen en belandt daardoor op de IC-afdeling van een ziekenhuis.
Hoe groter het reproductiegetal, hoe meer besmettingen en ook hoe meer bijkomende IC-patiënten. Lockdowns, evenals preventieve maatregelen zoals social distancing en het dragen van maskers, beperken het aantal besmettingen drastisch, en voorkomen daardoor ook dat de maximale IC-capaciteit niet overtroffen wordt.
Hoe groter het reproductiegetal, hoe meer besmettingen en ook hoe meer bijkomende IC-patiënten
Stel dat het reproductiegetal gelijk is aan 2. Het aantal besmette personen zal in een eerste besmettingsronde verdubbelen. Men kan dan verwachten dat het aantal patiënten dat op een IC-afdeling terechtkomt als gevolg van die eerste besmettingsronde ook verdubbelt.
Want 840 = 210 x 2 x 2. Het totaal aantal IC-patiënten is hoger want IC-patiënten verblijven langer op de IC dan de duurtijd van een besmettingsronde. Deze patiënten belanden pas op IC na een tweetal weken, waardoor IC-opnames achterlopen op de besmettingsronde.
Als we veronderstellen dat de voorbije besmettingsronde 210 nieuwe IC-patiënten opleverde, dan is het aantal nieuwe IC-patiënten in een eerstvolgende besmettingsronde ongeveer gelijk aan 210 x 2. Omdat nieuwe besmette personen op hun beurt weer mensen besmetten, is het aantal IC-patiënten ten gevolge van een tweede besmettingsronde gelijk aan 840 (zie extra).
Als we op die manier verder gaan, zien IC-afdelingen een stijging van 3360 patiënten na vier besmettingsrondes. Het aantal beschikbare IC-bedden is in Nederland ongeveer 1600, in België 1800. Het is duidelijk dat met een reproductiegetal van 2, we die capaciteit snel en drastisch overschrijden, met alle gevolgen van dien.
De strenge maatregelen hebben het reproductiegetal gelukkig doen dalen tot onder 1 en het scenario met een overbelasting van de IC-afdelingen werd daardoor afgewend. Als het reproductiegetal vandaag 0,8 is, zijn er na vier besmettingsrondes slechts 86 nieuwe IC-opnames.
De strenge maatregelen hebben het reproductiegetal doen dalen tot onder 1 en het scenario met een overbelasting van de IC-afdelingen afgewend
De exponentiële groei is beëindigd. Vele landen hebben intussen een pakket versoepelingen aangekondigd en gedeeltelijk doorgevoerd. We mogen bijvoorbeeld onze bubbel uitbreiden. Niet-essentiële handelszaken mogen opnieuw openen, sportwedstrijden kunnen hervat worden en de scholen zijn weer deels gestart.
Het reproductiegetal na vier besmettingsrondes stijgt opnieuw door deze versoepelingen, waardoor ook de druk op IC-afdelingen opnieuw toeneemt. Daarom is het belangrijk om voor elke geplande versoepeling eerst de verwachte stijging van het aantal IC-patiënten te schatten.
Een versoepeling te ver?
Veronderstel dat een eerste versoepelingsmaatregel, bijvoorbeeld het toelaten om twee bubbels samen te smelten, het reproductiegetal opnieuw doet stijgen van 0,8 naar 1,1. In plaats van 86 nieuwe IC-opnames stellen we er dan 307 vast na vier besmettingsrondes, zoals op de figuur hieronder te zien is.
Veronderstel dat er samen met de eerste maatregel nog een tweede versoepeling ingevoerd wordt, bijvoorbeeld het openen van niet-essentiële handelszaken, en dat het reproductiegetal door het gecombineerde effect van deze twee maatregelen stijgt met 0,6. Hierdoor bedraagt het aantal nieuwe IC- patiënten na vier rondes nu 807.
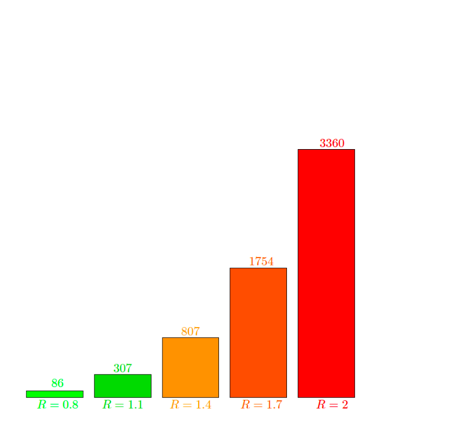
Merk op dat deze bijkomende versoepeling 500 extra IC-patiënten oplevert, terwijl als enkel de eerste maatregel zou ingevoerd worden er dat slechts 221 extra zijn. Het invoeren van drie gezamenlijke versoepelingsmaatregelen leidt tot 1754 nieuwe opnames en dikt het aantal IC-patiënten aan met 947.
Vier simultaan ingevoerde versoepelende maatregelen zorgen voor 3360 nieuwe IC-patiënten, een stijging van 1606 ten opzichte van drie gezamenlijk ingevoerde maatregelen! Hierbij veronderstelden we steeds dat iedere bijkomende maatregel zorgde voor een stijging van het reproductiegetal met 0,3.
De helft van de toename is enkel en alleen toe te schrijven aan de laatste versoepeling
Indien slechts één van de vier versoepelingsmaatregelen wordt ingevoerd, bedraagt de toename 221 IC-patiënten. Een naïeve en foutieve redenering schat het aantal IC-patiënten op 86 + 221 x 4 = 970 wanneer de vier versoepelingen tegelijk ingevoerd worden.
In werkelijkheid, zoals te zien op de figuur, is dat aantal gelijk aan 3360. De vier versoepelingen simultaan invoeren verhoogt het aantal IC-patiënten met 3274. Dat aantal is echter niet gelijk verdeeld over de verschillende versoepelingen. De helft van de toename is enkel en alleen toe te schrijven aan de laatste versoepeling!
Een convex effect
Wat is er hier aan de hand? Waarom is het effect van de gecombineerde versoepelingen niet gelijk aan de som van de effecten van stand-alone versoepelingen? De verklaring is dat een stijging in het reproductiegetal een convex effect heeft op het aantal nieuwe IC-patiënten waardoor de tol van een bijkomende versoepeling zwaarder wordt naargelang het aantal versoepelingen waarmee deze gecombineerd wordt.
Als we de IC-capaciteit schatten op ongeveer 1700 IC-bedden, wordt in geval van drie gecombineerde versoepelingsmaatregelen, de maximum capaciteit in ons fictieve voorbeeld al bereikt na vier besmettingsrondes.
Convexiteit impliceert dat de combinatie van ogenschijnlijk onschuldige versoepelingen desastreuse gevolgen kan hebben
Wie gelooft in het naïeve model denkt dat het invoeren van een viertal versoepelingen zorgt voor een kleine onderbezetting van de IC-afdelingen. Volgens deze naïeveling is de situatie dan kritiek, maar nog net haalbaar.
In werkelijkheid stort het gezondheidssysteem echter volledig in enkel en alleen door een bijkomende vierde versoepeling omdat door die extra versoepeling er plotseling slechts ruimte is voor de helft van de nieuwe IC-patiënten! Convexiteit impliceert dat de combinatie van ogenschijnlijk onschuldige versoepelingen desastreuse gevolgen kan hebben.
Daarom zijn spreiding en preventie bij de invoering van versoepelende maatregelen cruciaal. In plaats van vier simultane versoepelingen in te voeren is het veel veiliger om deze te spreiden in de tijd en te laten samengaan met bijkomende preventieve maatregelen, zoals het dragen van maskers en het snel opsporen van besmettingshaarden via een track & trace systeem bijvoorbeeld. Stel dat enkel de eerste versoepeling wordt ingevoerd: twee bubbels mogen samensmelten.
Tegelijk worden ook maskers verplicht en wordt bovendien een track & trace systeem geïmplementeerd. Pas na een aantal weken observeren we het netto-effect. Indien het reproductiegetal gelijk blijft aan 0,8, kan een tweede versoepeling ingevoerd worden. Het aantal IC-patiënten stijgt dan met 221, en niet met 500! Indien het reproductiegetal onverwacht stijgt na de eerste versoepeling, kan de tweede versoepeling uitgesteld worden, kunnen extra preventieve maatregen ingevoerd worden of kunnen bestaande maatregelen verbeterd worden.
Besluitvorming in onzekere tijden
We zijn ervan uitgegaan dat iedere versoepelingsmaatregel het reproductiegetal doet stijgen met 0,3. Dat is een louter fictieve keuze die we gemaakt hebben om de convexiteit te illustreren. In werkelijkheid proberen virologische en statistische modellen de echte stijging te voorspellen. Zelfs als een wiskundig model de 0,3 bevestigt, dan blijft dit slechts een gok, in het beste geval een goede gok. De onzekerheid, blijft altijd groot.
Omwille van die onzekerheid is het belangrijk om verschillende mogelijke scenario’s te onderzoeken. Op de onderstaande figuur correspondeert de blauwe lijn met het aantal IC-patiënten na vier besmettingsrondes wanneer de vier versoepelingen gezamenlijk doorgevoerd worden, voor verschillende waarden van de stijging in het reproductiegetal voor een individuele versoepeling. De groene verticale stippellijn markeert onze huidige schatting, waar iedere extra versoepelingsmaatregel een bijkomende toename van 0,3 in het reproductiegetal veroorzaakt.
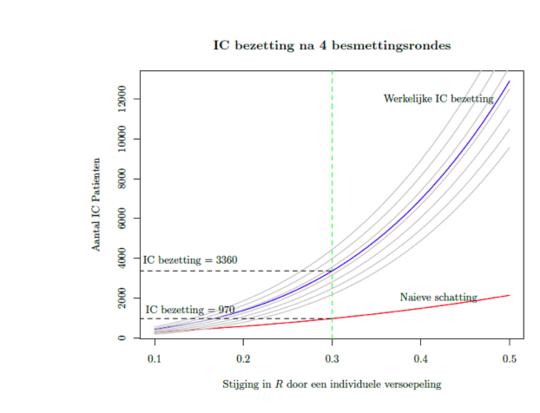
Modellen kunnen het ook bij het verkeerde eind hebben. Is de toename van het reproductiegetal werkelijk 0,3? Wat als het meer zou zijn? Om dit te onderzoeken, bewegen we ons over de blauwe lijn. Als we naar rechts gaan, klimmen we naar boven. Met andere woorden, als blijkt dat een versoepeling het reproductiegetal met meer dan 0,3 doet stijgen, dan onderschat ons model het aantal IC-patiënten, met alle mogelijke desastreuze gevolgen van dien!
Onzekerheid betekent echter ook dat het kan meevallen. De stijging van het reproductiegetal kan bijvoorbeeld slechts 0,2 bedragen, en in dat geval zijn er minder IC-patiënten dan verwacht.
Er is echter meer dan enkel de stijging! De curve is ook asymmetrisch. In het gunstige scenario, waar de versoepelingen een kleinere dan verwachte stijging van het reproductiegetal veroorzaken, worden we ‘beloond’ met minder IC-patiënten dan verwacht.
In het andere geval, waar blijkt dat we de stijging van het reproductiegetal door de ingevoerde versoepelingen hebben onderschat, is er een ‘afstraffing’: het aantal IC-patiënten is groter dan verwacht. Convexiteit impliceert dat de stijging van het aantal IC-patiënten door een te lage inschatting van het effect altijd groter is dan de daling van dit aantal door een (in absolute termen gelijke maar) te hoge inschatting. Of zoals het beschreven wordt door Nassim Taleb: "The pain will always be more than the gain!"
In onze bovenstaande berekeningen gingen we er van uit dat het huidige reproductiegetal gelijk is aan 0,8. De ‘correcte’ waarde van dat getal wordt bepaald aan de hand van beschikbare data en de inschattingen met betrekking tot de toekomstige verspreiding. De grijze lijnen in de figuur hierboven corresponderen met verscheidene mogelijke waarden voor het huidige reproductiegetal.
Wat we wel met zekerheid weten is dat de convexiteit ervoor zorgt dat te optimistische scenario’s vele malen nadeliger zijn dan te pessimistische scenario’s
De lijnen die boven de blauwe lijn liggen, gaan uit van een reproductiegetal dat hoger dan 0,8 ligt. Wanneer we naar rechts bewegen, drijven de verschillende lijnen uit elkaar, terwijl ze in de andere richting dichter bij elkaar komen te liggen. Als blijkt dat we het reproductiegetal te laag hebben ingeschat, onderschatten we ook het aantal IC-patiënten. Het effect daarvan is des te significanter naarmate we de stijging door de versoepelingen meer hebben onderschat.
Beter voorkomen dan genezen
We hebben hier te maken met twee onzekerheden. De onzekerheid omtrent de effectieve waarde van het huidige reproductiegetal en de onzekerheid betreffende de wijziging van dat reproductiegetal ten gevolge van de versoepelingen. Een onderschatting van het reproductiegetal en/of de wijziging ervan leidt tot een onderschatting van het aantal IC-patiënten. Een gecombineerde onderschatting leidt echter tot de meest dramatische scenario’s.
Extra data en onderzoek werken de hierboven besproken onzekerheden nooit helemaal weg. We moeten leven met deze onzekerheid, maar dat betekent niet dat we geen actie moeten ondernemen, wel dat beslissingen uitermate doordacht en stapsgewijs dienen te gebeuren. Stel dat er twijfel is of een bepaald pakket aan versoepelingen vervroegd kan doorgevoerd worden of niet.
Wees uitermate voorzichtig met het afbouwen van de lockdownmaatregelen en baseer geen beslissing op één scenario
We weten niet wat de toekomst precies brengt. Wat we wel met zekerheid weten is dat de convexiteit ervoor zorgt dat te optimistische scenario’s vele malen nadeliger zijn dan te pessimistische scenario’s. De belangrijkste les die we moeten onthouden is: wees uitermate voorzichtig met het afbouwen van de lockdownmaatregelen en baseer geen beslissing op één scenario.
Versoepelingsmaatregelen ofwel uitstellen ofwel koppelen aan preventieve maatregelen heeft tot doel het reproductiegetal onder 1 te houden en zodanig een tweede golf te vermijden. Het virus verdwijnt geleidelijk aan wanneer het reproductiegetal onder 1 ligt, maar flakkert snel op eens dat reproductiegetal opnieuw boven 1 uitstijgt. Door de convexiteit versnelt de opflakkering naarmate het reproductiegetal groter is.
Pas na gemiddeld twee weken wordt het werkelijke effect op het aantal besmettingen en de toegenomen druk op de IC-afdelingen duidelijk. Door voorzichtig te handelen vermijden we de situatie waarbij het reproductiegetal te snel en te ver boven 1 uitstijgt en zorgen we ervoor dat we verkeerde inschattingen alsnog kunnen bijsturen.




