
Als u met twee anderen in een kamer bent, is de kans dat minstens twee van de drie dezelfde verjaardag hebben erg klein – dat zien we intuïtief. (Het is minder dan 1%.) Maar hoeveel mensen moeten er in de kamer zijn opdat het bijna zeker is dat er minstens twee dezelfde verjaardag hebben – zeg maar, meer dan 99%?
Onze intuïtie zou ons kunnen vertellen dat het in de buurt van 99% van 365 moet liggen. Dat voelt immers mooi symmetrisch aan: met drie personen is het minder dan 1%, dus met 365-3 is het dan meer dan 99%. Maar tenzij u het antwoord kent, of een kei bent in kansrekening, kijkt u er wellicht van op dat het correcte antwoord 57 is. (Wikipedia gaat dieper in op de verjaardagenparadox.)
Wanneer minder waarschijnlijk meer waarschijnlijk lijkt
We zijn ook meestal niet zo schrander wanneer we moeten redeneren met relatieve waarschijnlijkheden, of dat is tenminste hoe het lijkt. Een van de moeilijker (zo niet meer controversiële) resultaten van het werk van psychologen Amos Tversky and Daniel Kahneman (die in 2002 de Nobelprijs Economie kreeg), staat bekend als de conjunctiedenkfout (of 'conjunction fallacy').
Dit is een formele denkfout, waarbij men besluit dat een meer specifieke uitspraak (bv. waarin twee voorwaarden in conjunctie gelden – “mijn vriend heeft een zus die An heet”) meer waarschijnlijk is dan een meer algemene (bv. waarin slechts een voorwaarde geldt – “mijn vriend heeft een zus”).
Het canonieke voorbeeld dat we aan Tversky en Kahneman hebben te danken is dat van Linda, een hypothetische dame van 31, waarover ons enkele feiten worden verteld. Dan wordt ons gevraagd wat meer waarschijnlijk is: (a) ze is een bankbediende, of (b) ze is een bankbediende én actief als feministe.
De waarschijnlijkheidsleer is duidelijk: (b) is meer specifiek, en kan dus hooguit even waarschijnlijk zijn als (a) (daarvoor moeten dan alle vrouwelijke bankbedienden feminist zijn). Nochtans stelden Tversky en Kahneman vast dat 85% van hun deelnemers in hun onderzoek dachten dat (b) meer waarschijnlijk was dan (a).
Critici van de gedragseconomie, zoals Gerd Gigerenzer, beweren dat dit helemaal geen fout is. In de normale omgang gebruiken mensen het begrip waarschijnlijkheid immers niet noodzakelijk in de wiskundige zin. Als de informatie over Linda het plausibel maakt dat ze feminist is, interpreteren we dit gemakkelijk als een aanwijzing van waarschijnlijkheid.

We kunnen makkelijk andere voorbeelden verzinnen. Beeld u bijvoorbeeld Jef in: hij verlaat het café op weg naar huis. Hij heeft een biertje of twee gedronken met de collega’s en het alcoholgehalte in zijn bloed is net boven de wettelijke limiet.
Wat is meer waarschijnlijk: (a) hij rijdt huiswaarts in een witte auto, of (b) hij rijdt huiswaarts in een witte auto en raakt bij het parkeren op de oprit het tuinmuurtje? Zelfs als u, door wat u net las, op weg bent gezet om het correcte antwoord geven, voelt u vermoedelijk toch de intuïtieve drang het verkeerde, maar plausibele antwoord te geven, net omdat het zo juist aanvoelt.
Maar de denkfout treedt niet enkel op in situaties waar de spreektaal de starre regels van het redeneren rond kansen vertroebelt. In een ander experiment vroegen Tversky en Kahneman de deelnemers zich een normale teerling voor te stellen met vier groene en twee rode vlakken. Die zou 20 keer worden gerold, en de opeenvolgende uitkomsten zouden worden genoteerd als G en R. Ze konden vervolgens een van drie korte sequenties kiezen, en als hun keuze voorkwam in de opeenvolging van 20 worpen, zouden ze 25 dollar winnen – ze hadden dus een stimulans om de correcte keuze te maken.
De drie opties waren (a) RGRRR, (b) GRGRRR en (c) GRRRRR. Scherpzinnige lezers hebben beslist al gemerkt dat sequentie (a) vervat zit in sequentie (b), en dus een grotere kans heeft om voor te komen. Toch kozen 65% van de deelnemers de minder waarschijnlijke optie (b), ondanks het feit dat dit hun kansen op het winnen van 25 dollar ongeveer halveerde.
Een bonus is niet genoeg
Maar goed, 65% was toch al minder dan de 85% die de het verkeerde antwoord gaven over Linda, dus misschien geven we meer accurate antwoorden als er geld mee gemoeid is.
Gary Charness, Edi Karni en Dan Levin, drie economen, onderzochten of zo’n financiële aansporing ook tot een beter resultaat bij het Linda-vraagstuk zou leiden. Aan de controlegroep in hun experiment werd geen stimulans aangeboden, maar zij kregen 2 dollar wanneer ze de hogervermelde vraag over Linda beantwoordden.
De deelnemers in de behandelgroep vernamen dat er een correct antwoord was, en dat eenieder die dat zou kiezen een bonus van 4 dollar zou ontvangen. Het experiment werd in drie vormen uitgevoerd: individueel, als duo’s en als trio’s.
De onderzoekers slaagden er niet in de het resultaat van Tversky en Kahneman (85% ‘fout’) te repliceren, maar toch gaven 58% van de individuele deelnemers in de controlegroep het verkeerde antwoord. Het vooruitzicht op een financiële bonus bracht dit echter terug tot 33%. En dat was niet alles: wanneer de deelnemers samenwerkten koos slechts 48% (in duo’s) en 26% (in trio’s) van de deelnemers het ‘foute’ antwoord in de controlegroep. Met de belofte op een bonus zakte dat aandeel respectievelijk tot 13% en 10%.
Het overtreden van de conjunctieregel verdween niet geheel – een derde van de deelnemers in de individuele versie liet 4 dollar aan zich voorbijgaan door vol te houden dat het meer waarschijnlijk was dat Linda een feministische bankbediende was dan dat ze een bankbediende was. Maar het effect van de samenwerking was dan wel weer markant.
Het probleem blijft wetenschappers alvast bezighouden: het is nog steeds wat mysterieus dat we een relatief eenvoudige basisregel overtreden, en zo mogelijk nadelige beslissingen nemen. Recent bogen twee filosofen aan de universiteit van Oxford, Kevin Dorst en Matt Mandelkern, zich over het meer algemene fenomeen van gissingen, en zij schuiven een originele verklaring naar voren voor de conjunctiedenkfout.
Een fout die niet onjuist is
Hun hypothetische figuur is Latif, een jongeman die aanvaard is door de rechtsfaculteiten van alle vier Amerikaanse topuniversiteiten. We weten niets over zijn voorkeuren, maar eerdere gelijkaardige kandidaten kozen volgens een gegeven verdeling: Yale (38%), Stanford (30%), Harvard (20%) en NYU (12%).
Welk antwoord zou men geven op de vraag waar Latif rechten zal gaan studeren? Naast, uiteraard, nauwkeurigheid, identificeerden de onderzoekers een tweede eigenschap van een antwoord: informativiteit (hoe specifiek is het). Het antwoord “Latif zal naar Yale, Stanford, Harvard of NUY gaan” is bijvoorbeeld 100% nauwkeurig, maar niet informatief, want we weten al dat hij een van deze vier universiteiten zal kiezen.
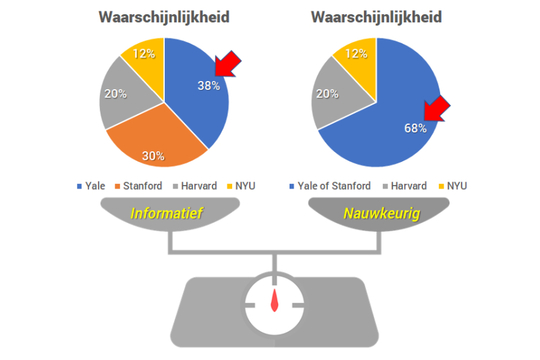
Dorst en Mandelkern stellen dat mensen een afweging maken tussen nauwkeurigheid en informativiteit. Deze twee facetten concurreren rechtstreeks met elkaar: een meer specifiek antwoord heeft een grotere kans verkeerd te zijn.
“Latif zal naar Yale gaan” is meer informatief (maar minder waarschijnlijk), terwijl “Latif zal naar Yale of naar Stanford gaan” meer waarschijnlijk is (maar minder informatief).
Wanneer ze gissen, streven mensen naar het optimaliseren van de algemene waarde van het antwoord, waarin zowel precisie als informativiteit zitten vervat. Dit kan leiden tot een geprefereerd antwoord dat niet het meest nauwkeurige is, maar waarin dat gemis wordt gecompenseerd doordat het meer informatie verschaft. (Dit idee wordt verder uitgewerkt in de paper, en er is ook een blogpost waarin ze dit specifieke aspect bespreken.)
Dit inzicht lijkt een plausibele verklaring voor wat tot dusver werd beschouwd als een denkfout: als nauwkeurigheid niet het enige is wat van belang is, dan mis je natuurlijk een deel van het plaatje als je je oordeel over een beslissing enkel daarop baseert. Het is ook een mooie illustratie van de onmetelijke rijkdom van de menselijke gedachten.
Maar is hiermee het laatste woord gezegd over de conjunctiedenkfout? Ik ben er niet zo zeker van. Wat denkt u?
Is het meer waarschijnlijk dat (a) het debat rond deze controverse verdergaat, of (b) het debat rond deze controverse verdergaat én het afwegingsinzicht van Dorst en Mandelkern wordt bevestigd als een degelijke verklaring?




