‘Nil Volentibus Arduum’ was het nieuwe letterwoord dat Bart De Wever toedichtte aan zijn partij, de Nieuw-Vlaamse Alliantie of N-VA. Door de Latijnse woorden klonk het geheel plechtstatig en verrassend, zoals paste bij een overwinningstoespraak. Ondertussen hebben we de Latijnse spreuken wel gehad, en omdat een verrassende kwinkslag een sleutelelement is bij redenaarskunst, schijnt De Wever nu de wiskunde te gebruiken (of te misbruiken, naargelang de politieke overtuiging).
Dichterlijke overdrijving
Inderdaad, in het debat over de Lange ex-Wapper, maakte Ivan De Vadder in De zevende dag een toespeling op een zoveelste oneliner van de N-VA-voorzitter toen het ging over de kostprijsberekening: "Je moet de geschatte kostprijs altijd vermenigvuldigen met de pi-factor (pi = 3,14) om in de buurt te komen van de uiteindelijke prijs."
Het getal pi, de omtrek van een cirkel gedeeld door zijn diameter, heeft niets te maken met de berekening van de bewuste kostprijs. Bart wou eenvoudigweg zeggen dat een geschatte aanbesteding bij openbare bouwwerken dikwijls wordt overschreden, en twee- tot driemaal zo groot kan worden als de originele prijs. Met enige dichterlijke overdrijving, want pi is iets meer dan drie.
Pseudowiskunde
Bovendien komt het in wis- of natuurkundige kringen erg veel voor om te zeggen dat een formule met "een factor pi wordt vermenigvuldigd", want het is een soort wiskundige 'staande uitdrukking’. Het gebruik van de lievelingsconstante van de wiskunde buiten haar context geeft weer iets plechtigs, ditmaal passend bij de verwezenlijking van een groot bouwwerk. Echter, hoever kan men wiskundige verwijzingen doorduwen vooraleer ze vervallen in pijnlijke overdrijvingen?
Het gebruik van een wiskundige verwijzing als demagogisch element is ouder dan men zou denken. In De wiskundige Ervaring (1981) geven de auteurs Philip J. Davis en Reuben Hersh hiervan voorbeelden. Zij reiken van de verzonnen stadslegende over de Zwitserse wiskundige Leonhard Euler, die een wiskundige formule gebruikte om de Franse filosoof Denis Didérot te overbluffen, tot het doorprikken van de pseudowiskunde van de beroemde Samuel Huntington, auteur van Clash of Civilisations en Political Order in Changing Societies. Ook is humor met wiskundige symbolen geen vondst van Bart De Wever: een bekende nerdgrap ontstaat bijvoorbeeld door gebruik te maken van de logische symbolen \/ voor ‘of’ en ‘N’ voor ‘negatie’, waardoor een bekende uitspraak van Shakespeare zich laat schrijven als: 2B \/ N(2B).
Geldstroom
Terug naar de actualiteit en de bijzondere financieringswet, die de bedragen bepaalt die de verschillende overheden in België krijgen. In de jaren tachtig maakten de zogenaamde 'Toshiba-boys' van Jean-Luc Dehaene furore, omdat zij op hun Toshiba-laptops als enigen over de onderhandelde modellen beschikten en zo een unieke machtspositie innamen. Nu iedereen over een flashy laptop beschikt, proberen de zogenaamde ‘delta-boys’ het opnieuw, zij het nu door flashy formules (zie het document van Frank Vandenbroucke en Lieven Meert, .pdf).
De illustratie toont een dergelijke formule. Het doet er hier weinig toe waar alle symbolen voor staan, de aanblik zegt genoeg. Let wel, hierin verwijzen de indices GER, FRA en NED niet naar de Duits-, Frans- of Nederlandstalige Gemeenschap, maar naar buurlanden. Immers, voor het Brusselse, Vlaamse of Waalse Gewest gebruiken de ‘delta-boys’ de index i; zij zeggen dus dat "iemand woont in het i-de Gewest, waarbij i = 1, 2 of 3". Zo stelt Bt,i de geldstroom voor naar Gewest i in het jaar t. Is het toeval dat B ook de eerste letter is van België?
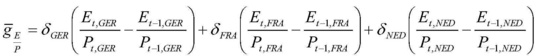
Kleine gestalte
Dat enige wiskundige demagogie de auteurs van deze formules niet vreemd is, toont een vergelijking met andere formules: soms gebruiken ze het vermenigvuldigingsteken ‘×’ wel, soms niet. In de formules met de vele delta’s staat geen enkel vermenigvuldigingsteken, en een leek vraagt zich wellicht af hoe ‘alles aan elkaar hangt’. Beroepswiskundigen gebruiken het teken nooit, tenzij uit vriendelijkheid voor de wiskundige analfabeet of uit een soort minachtende spot, want het aanbrengen ervan wordt gezien als ‘baby math’.
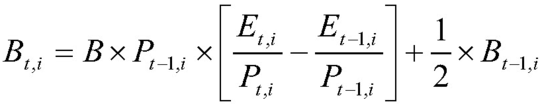
De keuze van de letters geeft ook inhoudelijke aanwijzingen. De kleine Griekse letter delta, δ, staat voor een ‘kleine’ toename (of afname, als het getal negatief is), al is het rekbaar wat men hierbij onder ‘klein’ verstaat. Soms worden ook de hoofdletter delta, Δ, gebruikt, of de letter die alfabetisch na delta komt, de epsilon, ε. Nerds dichten iemand van kleine gestalte al eens de bijnaam ‘epsilon’ toe. De keuze voor de letters voor de voorziene toenames, δ, getuigt dus onbewust van een erg voorzichtige benadering van de hervorming van de financieringswet!
De peer in alfa snijden
Soms is de uitleg van de deltaboys op zijn minst verwarrend. Enerzijds staat er:
Aangezien de totale bonus die een gewest krijgt voor één activering gelijk is aan B/(1-epsilon), krijgt elk gewest 10.000 euro van de federale overheid voor een duurzame activering. Deze 10.000 euro wordt evenwel gespreid in de tijd. 5.000 euro krijgt het gewest onmiddellijk. De jaren nadien 2.500, 1.250, 625,… zodat de totaalsom 10.000 euro is.
En anderzijds:
Epsilon: parameter tussen 0 en 1, geeft de mate aan waarin de bonus wordt uitgesmeerd in de tijd. […] Indien epsilon gelijk is aan 1, dan wordt het systeem cumulatief. Het verliest dan zijn tijdelijk karakter.
Nu, snel wordt die totaalsom niet bereikt, zelfs al is epsilon één half zoals in het voorbeeld: 5.000; 2.500; 1.250; 625; 312,5; 156,25; 78,125; 39,06…; 19,53…; 9,76…; 4,88… en na tien jaar dient er nog altijd zowat 5 euro te worden gestort, en dat vermenigvuldigd met de enorme schaal waar het in werkelijkheid over gaat. Zo tijdelijk is het allemaal niet. Erger nog, ons inziens wordt de noemer nul in de uitdrukking ‘B/(1-epsilon)’ indien epsilon 1 is. Een deling door nul mag niet in de wiskunde, maar misschien wel in de politiek.
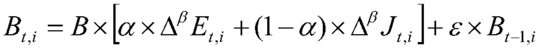
Leuk is dan weer de vondst van de compromisfactor. Uit dagdagelijkse discussies kent men de uitdrukking ‘we snijden de peer in twee’, maar de deltaboys doen natuurlijk beter. Zij ‘snijden de peer in alfa’: als in ‘alfa × peer + (1- alfa) × peer’ alfa gelijk is aan ½, is de peer inderdaad in twee helften gesneden.
Acceleratio
Maar als alfa gelijk is aan 1/3 is het andere deel 1- 1/3 = 2/3. Of, als alfa 0,314… is, is 1-alfa = 0,686. In het eerste geval is de peer in 1/3+2/3 gesneden, in het tweede in 0,314…+0,686…
Of, om het met de woorden van de onderhandelaars te zeggen:
Maar we kunnen leven met compromissen tussen beide indicatoren, in de vorm van een gewogen gemiddelde (met α tussen 0 en 1).
Tot slot hebben we met de aanslepende regeringsonderhandelingen en de nieuwe wiskundige demagogische tendens een suggestie voor Bart De Wever. Immers, ‘v’ staat in de wiskunde voor ‘snelheid’ (van, jawel, het Latijnse ‘velocitas’) en ‘a’ voor ‘versnelling’ (van ‘acceleratio’), maar de onderhandelingen worden vooral gekenmerkt door hun negatie, of, in een wiskundige schrijfwijze: ‘N(v,a)’: geen snelheid noch versnelling, het gaat niet vooruit.




